Расчет оптимальной интенсивности поступления транспортных средств в транспортно-грузовую систему

Поступление транспортных средств к местам погрузки - выгрузки происходит стохастически, то есть через случайные промежутки времени. Продолжительность выполнения грузовых операций с каждой транспортной единицей зависит от рода груза, типа ПС и также является стохастической величиной.

Коэффициент загрузки транспортно-грузовой системы по времени представляет собой отношение интенсивности прибытия ТС в единицу времени (λ) к интенсивности обслуживания (m):

a= λ /m, (λ<1).

Параметр a характеризует степень использования ПРМ по времени и представляет собой долю времени (час, смена, сутки), в течение которого ПРМ занят выполнением грузовых операций. Величина a оказывает большое влияние на экономическую сторону транспортно-грузовых процессов. С увеличением a сокращаются издержки простоя ПРМ, резко увеличиваются издержки от простоя ТС в ожидании начала грузовых операций и наоборот.

Таким образом, в курсовой работе необходимо рассмотреть оптимальную величину a, при которой издержки от простоя ПРМ и ПС будут минимальными.

В общем виде уравнение издержек, связанных с простоем ПРМ и ПС, имеет вид:

И=Иваг+Ипрм, 4.3

где Иваг- издержки от простоя ТС в ожидании начала грузовых операций;

Ипрм -издержки от простоя ПРМ.

Когда ТС прибывают в транспортно-грузовую систему случайным образом, издержки от простоя ТС в соответствии с теорией массового обслуживания определяются по формуле:

Иваг=nСваг 4.4

где n - среднее количество транспортных единиц (вагонов), находящихся в очереди;

Сваг- стоимость простоя вагона.

Издержки от простоя ПРМ определяются по формуле:

Ипрм=Спрм(1-a), 4.5

где Спрм- стоимость простоя ПРМ за 1 час.

Тогда:

И=nСваг + Спрм(1-a), 4.6

Если поток ТС является Пуассоновским, обслуживание ТС (время выполнения транспортных операций) - Эрланговским, то величина n будет иметь вид:

n=a2(1+1/k)/2(1-a) 4.7

Взяв первую производную dИ/dk и приравняв ее к 0, найдем a, при котором создадутся минимальные издержки от простоя ТС и ПРМ:

a= 4.8

Подставляя заданные значения Сваг , Спрм и k в формулы 4.7, 4.8 получим:

a=;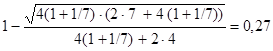

n=.

В этом случае оптимальная интенсивность поступления вагонов в транспортно-грузовую сеть будет равна:

l=m*a 4.9

l=3·0,27=0,81 ваг/час.

Если принять за критерий оптимизации максимальное количество отгружаемых вагонов при минимальных издержках от простоя, то есть оптимум будет находиться из условия минимальных издержек от простоя на 1 отгруженный вагон, то коэффициент a и m будут другими.

При a==0,27 и m=3 суммарные издержки от простоя составят:

И=0,057·4+7·(1-0,27)=5,34 д.е.

На каждый отгруженный вагон издержки от простоя составят:

Ио=И/m*a=И/l 4.10

Ио=5,34/0,81=6,59 д.е./ваг.

На рисунке 4.3 изображена зависимость издержек простоя ПРМ и ПС от величины загрузки транспортно- грузовой системы.

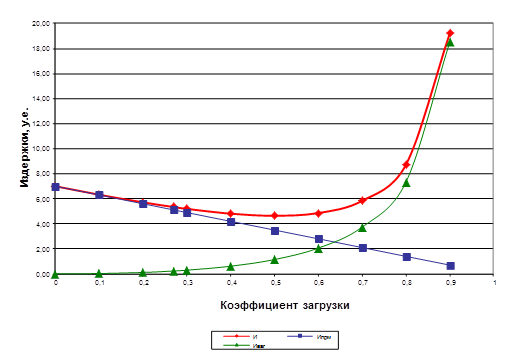
Рисунок 4.3 – Зависимость издержек простоя ПРМ и ПС от загрузки транспортно-грузовой системы

Популярные материалы:

Построение внешней скоростной характеристики
Внешняя скоростная характеристика двигателя необходима для получения тяговой характеристики автомобиля. Наиболее точно внешнюю скоростную характеристику вновь проектируемого двигателя можно построить по результатам теплового расчета, пров ...

Правила плавания
Статья 1. Загрязнением моря нефтью и нефтеводяной смесью считается любой их слив в море с содержанием нефти более 100 J1iг на 1 л воды. Статья 2. Если слив нефти или нефтеводяной смеси произведен с судна, то ответственным лицом за загряз ...

Рулевое управление
Тип рулевого управления Травмобезопасный Рулевой механизм Шестерня—рейка Рулевой привод Две тяги с резинометаллическими шарнирами со стороны рулевого механизма и шаровыми шарнирами со стороны поворотных рычагов ...