Составление дифференциального уравнения вынужденных колебаний подпрыгивания вагона

Решение дифференциального уравнения n = 2p/Т является аналитическим выражением процесса вынужденных колебаний подпрыгивания вагона при движении его по регулярным неровностям вида z = hcoswt.

Это решение имеет вид:

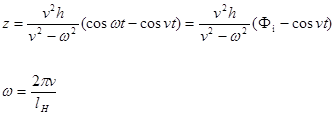
где n - скорость движения вагона;

lн – длинна периода неровностей;

2h – высота неровностей;

n - круговая частота собственных колебаний

Для колеса вагона номер i возмущение функции имеет вид:

где li – расстояние от первого до i-го колеса.

Амплитуда вынужденных колебаний подпрыгивания кузова вагона будет иметь вид:

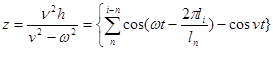
Для заданного вагона

Аналитическое выражение описывающее процесс вынужденных колебаний будет иметь вид:

Для построения графика определяем зависимость z от t

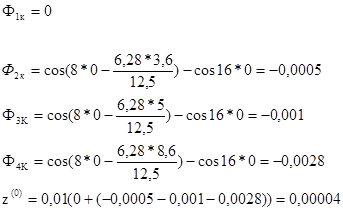
При t=1 сек

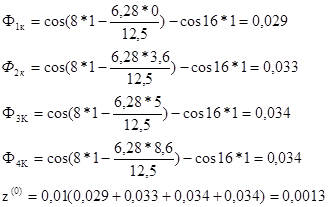
Для других значений t

Популярные материалы:

Определение специализации, производственной мощности и размеров вагоносборочного участка депо
Место размещения депо выбираем на сортировочной станции. Годовая программа деповского ремонта, с учетом возможности увеличения плана ремонта в перспективе, Nд, вагонов, вычисляют по формуле: (24) где: kр - коэффициент, учитывающий рез ...

Анализ себестоимости ремонта вагонов и расходов на ремонт колесных пар
Себестоимость деповского ремонта в 1 полугодии т.г. по сравнению с прошлым годом снизилась по полувагонам и платформам Себестоимость ремонта полувагонов в среднем составляет 3,5 млн. рублей и сократилась на 3,7% к 1996 году. Выше средне ...

Возможные регулировки системы
Одной из причин ухудшения динамики автомобиля во время разгона является нарушение работы ускорительного насоса. Правильность работы ускорительного насоса проверить очень просто. Проверяют работу ускорительного насоса при снятой крышке кар ...